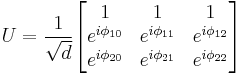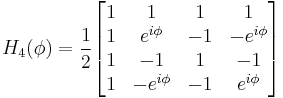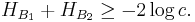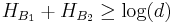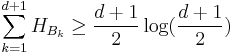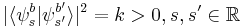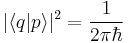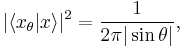Mutually unbiased bases
In quantum information theory, mutually unbiased bases in Hilbert space Cd are two orthonormal bases  and
and  such that the square of the magnitude of the inner product between any basis states
such that the square of the magnitude of the inner product between any basis states 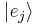 and
and 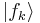 equals the inverse of the dimension d:[1]
equals the inverse of the dimension d:[1]
These bases are unbiased in the following sense: if a system is prepared in a state belonging to one of the bases, then all outcomes of the measurement with respect to the other basis will occur with equal probabilities.
Contents |
Overview
The notion of mutually unbiased bases was first introduced by Schwinger in 1960,[2] and the first person to consider applications of mutually unbiased bases was Ivanovic[3] in the problem of quantum state determination.
Another area where mutually unbiased bases can be applied is quantum key distribution, more specifically in secure quantum key exchange.[4] Mutually unbiased bases are used in many protocols since the outcome is random when a measurement is made in a basis unbiased to that in which the state was prepared. When two remote parties share two non-orthogonal quantum states, attempts by an eavesdropper to distinguish between these by measurements will affect the system and this can be detected. While many quantum cryptography protocols have relied on 1-qubit technologies, employing higher dimensional states, such as qutrits, allows for better security against eavesdropping.[4] This motivates the study of mutually unbiased bases in higher-dimensional spaces.
Other uses of mutually unbiased bases include quantum state reconstruction,[5] quantum error correction codes,[6][7] and the so called "mean king's problem".[8][9]
Existence problem
Let 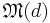 denote the maximal number of mutually unbiased bases in the d-dimensional Hilbert space Cd. It is an open question[10] how many mutually unbiased bases,
denote the maximal number of mutually unbiased bases in the d-dimensional Hilbert space Cd. It is an open question[10] how many mutually unbiased bases, 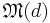 , one can find in Cd, for arbitrary d.
, one can find in Cd, for arbitrary d.
In general, if
is the prime number decomposition of d, where
then the maximal number of mutually unbiased bases which can be constructed satisfies[1]
It follows that if the dimension of a Hilbert space d is an integer power of a prime number, then it is possible to find d + 1 mutually unbiased bases. This can be seen in the previous equation, as the prime number decomposition of d simply is 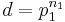 . Therefore,
. Therefore,
Though the maximal number of mutually unbiased bases is known when d is an integer power of a prime number, it is not known for arbitrary d.
Examples of sets of mutually unbiased bases
Example for d = 2
The three bases
provides the simplest example of mutually unbiased bases in C2. The above bases are composed of the eigenvectors of the Pauli spin matrices 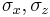 and their product
and their product 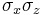 .
.
Example for d = 4
For d = 4, an example of d + 1 = 5 mutually unbiased bases where each basis is denoted as Mj, 0 ≤ j ≤ 4, is given as follows:[11]
Methods for finding mutually unbiased bases
Weyl group method[1]
Let 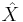 and
and 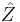 be two unitary operators in the Hilbert space Cd such that
be two unitary operators in the Hilbert space Cd such that
for some phase factor  . If
. If  is a primitive root of unity, for example
is a primitive root of unity, for example 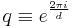 then the eigenbases of
then the eigenbases of 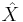 and
and 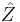 are mutually unbiased.
are mutually unbiased.
By choosing the eigenbasis of 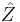 to be the standard basis, we can generate another basis unbiased to it using a Fourier matrix. The elements of the Fourier matrix are given by
to be the standard basis, we can generate another basis unbiased to it using a Fourier matrix. The elements of the Fourier matrix are given by
Other bases which are unbiased to both the standard basis and the basis generated by the Fourier matrix can be generated using Weyl groups.[1] The dimension of the Hilbert space is important when generating sets of mutually unbiased bases using Weyl groups. When d is a prime number, then the usual d + 1 mutually unbiased bases can be generated using Weyl groups. When d is not a prime number, then it is possible that the maximal number of mutually unbiased bases which can be generated using this method is 3.
Unitary operators method using Galois fields [12]
When d = p is prime, we define the unitary operators 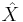 and
and 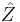 by
by
where 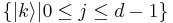 is the standard basis and
is the standard basis and 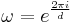 is a root of unity.
is a root of unity.
Then the eigenbases of the following d + 1 operators are mutually unbiased:[12]
When 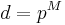 is a power of a prime, we make use of the Galois field
is a power of a prime, we make use of the Galois field 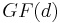 to construct a maximal set of d + 1 mutually unbiased bases. We label the elements of the computational basis of Cd using the Galois field:
to construct a maximal set of d + 1 mutually unbiased bases. We label the elements of the computational basis of Cd using the Galois field: 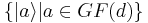 .
.
We define the operators 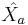 and
and 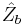 in the following way
in the following way
where
and the addition and multiplication in the kets and 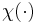 is that of
is that of 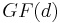 .
.
Then we form d + 1 sets of commuting unitary operators:
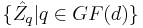 and
and 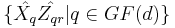 for each
for each 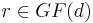
The joint eigenbases of the operators in one set are mutually unbiased to that of any other set.[12] We thus have d + 1 mutually unbiased bases.
Hadamard matrix method[1]
Given that one basis in a Hilbert space is the standard basis, then all bases which are unbiased with respect to this basis can be represented by the columns of a complex Hadamard matrix multiplied by a normalization factor. For d = 3 these matrices would have the form
The problem of finding a set of k+1 mutually unbiased bases therefore corresponds to finding k mutually unbiased complex Hadamard matrices.
An example of a one parameter family of Hadamard matrices in a 4 dimensional Hilbert space is
The problem of finding a maximal set of MUBs when d = 6
The smallest dimension that is not an integer power of a prime is d = 6. This is also the smallest dimension for which the number of mutually unbiased bases is not known. The methods used to determine the number of mutually unbiased bases when d is an integer power of a prime number cannot be used in this case. Searches for a set of four mutually unbiased bases when d = 6, both by using Hadamard matrices[1] and numerical methods[13] have been unsuccessful. The general belief is that the maximum number of mutually unbiased bases for d = 6 is 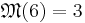 .[1]
.[1]
Entropic Uncertainty Relations and MUBs
There is an alternative characterization of mutually unbiased bases that considers them in terms of uncertainty relations.[14]
Entropic uncertainty relations are analogous to the Heisenberg uncertainty principle, and Maassen and Uffink[15] found that for any two bases 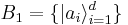 and
and 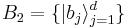 :
:
where 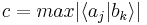 and
and 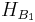 and
and 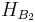 is the respective entropy of the bases
is the respective entropy of the bases 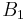 and
and 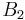 , when measuring a given state.
, when measuring a given state.
Entropic uncertainty relations are often preferable[16] to the Heisenberg uncertainty principle, as they are not phrased in terms of the state to be measured, but in terms of c.
In scenarios such as quantum key distribution, we aim for measurement bases such that full knowledge of a state with respect to one basis implies minimal knowledge of the state with respect to the other bases. This implies a high entropy of measurement outcomes, and thus we call these strong entropic uncertainty relations.
For two bases, the lower bound of the uncertainty relation is maximized when the measurement bases are mutually unbiased, since mutually unbiased bases are maximally incompatible: the outcome of a measurement made in a basis unbiased to that in which the state is prepared in is completely random. In fact, for a d-dimensional space, we have:[17]
for any pair of mutually unbiased bases 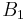 and
and 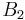 . This bound is optimal[18]: If we measure a state from one of the bases then the outcome has entropy 0 in that basis and an entropy of
. This bound is optimal[18]: If we measure a state from one of the bases then the outcome has entropy 0 in that basis and an entropy of 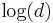 in the other.
in the other.
If the dimension of the space is a prime power, we can construct d + 1 MUBs, and then it has been found that[19]
which is stronger than the relation we would get from pairing up the sets and then using the Maassen and Uffink equation. Thus we have a characterization of d + 1 mutually unbiased bases as those for which the uncertainty relations are strongest.
Although the case for two bases, and for d + 1 bases is well studied, very little is known about uncertainty relations for mutually unbiased bases in other circumstances.[19] [20]
When considering more than two, and less than 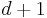 bases it is known that large sets of mutually unbiased bases exist which exhibit very little uncertainty [21]. This means merely being mutually unbiased does not lead to high uncertainty, except when considering measurements in only two bases. Yet there do exist other measurements that are very uncertain[19][22].
bases it is known that large sets of mutually unbiased bases exist which exhibit very little uncertainty [21]. This means merely being mutually unbiased does not lead to high uncertainty, except when considering measurements in only two bases. Yet there do exist other measurements that are very uncertain[19][22].
Mutually unbiased bases in infinite dimension Hilbert spaces
While there has been investigation into mutually unbiased bases in infinite dimension Hilbert space, their existence remains an open question. It is conjectured that in a continuous Hilbert space, two orthonormal bases 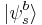 and
and 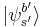 are said to be mutually unbiased if[23]
are said to be mutually unbiased if[23]
For the generalized position and momentum eigenstates 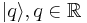 and
and 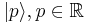 , the value of k is
, the value of k is
The existence of mutually unbiased bases in a continuous Hilbert space remains open for debate, as further research in their existence is required before any conclusions can be reached.
Position states 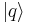 and momentum states
and momentum states 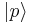 are eigenvectors of Hermitian operators
are eigenvectors of Hermitian operators 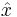 and
and 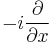 , respectively. Weigert and Wilkinson [23] were first to notice that also a linear combination of these operators have eigenbases, which have some features typical for the mutually unbiased bases. An operator
, respectively. Weigert and Wilkinson [23] were first to notice that also a linear combination of these operators have eigenbases, which have some features typical for the mutually unbiased bases. An operator 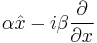 has eigenfunctions proportional to
has eigenfunctions proportional to 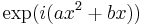 with
with 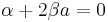 and the corresponding eigenvalues
and the corresponding eigenvalues 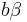 . If we parametrize
. If we parametrize  and
and  as
as 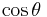 and
and 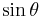 , the overlap between any eigenstate of the linear combination and any eigenstate of the position operator (both states normalized to the Dirac delta) is constant, but dependent on
, the overlap between any eigenstate of the linear combination and any eigenstate of the position operator (both states normalized to the Dirac delta) is constant, but dependent on  :
:
where 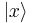 and
and 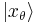 stand for eigenfunctions of
stand for eigenfunctions of 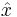 and
and 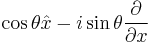 .
.
References
- ^ a b c d e f g I. Bengtsson, Three ways to look at mutually unbiased bases, http://arxiv.org/abs/quant-ph/0610216.
- ^ J. Schwinger, Unitary Operator Bases, Harvard University, 1960, http://www.pubmedcentral.nih.gov/picrender.fcgi?artid=222876&blobtype=pdf.
- ^ I. D. Ivanovic, J. Phys. A. 14. 3241 (1981).
- ^ a b M. Planat et al, A Survey of Finite Algebraic Geometrical Structures Underlying Mutually Unbiased Quantum Measurements, http://hal.ccsd.cnrs.fr/docs/00/07/99/18/PDF/MUB_FP.pdf.
- ^ W. K. Wootters and B. D. Fields, Optimal State-Determination by Mutually Unbiased Measurements, Ann. Phys. 191 (1989) 363-381.
- ^ D. Gottesman, Class of quantum error-correcting codes saturating the quantum Hamming bound, Phys. Rev. A 54 (1996) 1862-1868.
- ^ A. R. Calderbank et al, Quantum Error Correction and Orthogonal Geometry, Phys. Rev. Lett. 78 (1997) 405-408.
- ^ L. Vaidman et al, How to ascertain the values of
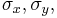 and
and 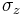 of a spin-1/2 particle, Phys. Rev. Lett. 58 (1987) 1385-1387.
of a spin-1/2 particle, Phys. Rev. Lett. 58 (1987) 1385-1387. - ^ B.-G. Englert and Y. Aharonov, The mean king’s problem: prime degrees of freedom, Phys. Lett. A 284 (2001) 1-5.
- ^ T. Durt, B.-G. Englert, I. Bengtsson, K. Życzkowski, "On mutually unbiased bases", Int. J. Quantum Information, 8, 535-640 (2010), http://arxiv.org/abs/1004.3348.
- ^ A. Klappenecker, M. Roetteler, Constructions of Mutually Unbiased Bases, 2003, http://arxiv.org/abs/quant-ph/0309120.
- ^ a b c S. Bandyopadhyay, P. O. Boykin, V. Roychowdhury, F. Vatan, A new proof for the existence of mutually unbiased bases, 2001, http://arxiv.org/abs/quant-ph/0103162.
- ^ P. Butterley, W. Hall, Numerical evidence for the maximum number of mutually unbiased bases in dimension six, 2007, http://arxiv.org/abs/quant-ph/0701122.
- ^ I.I. Hirschman, Jr., A note on entropy. American Journal of Mathematics (1957) pp. 152–156.
- ^ H. Maassen, J.B.M. Uffink: Generalized entropic uncertainty relations: Phys. Rev. Lett. 60, 1103–1106 (1988).
- ^ I. Damgard, S. Fehr, R. Renner, L. Salvail, C. Schaner(2006), http://arxiv.org/abs/quant-ph/0612014.
- ^ D. Deutsch, Uncertainty in Quantum Measurements. Physical Review Letters, 50(9):631–633, February 1982.
- ^ A. Ambainis, Limits on entropic uncertainty relations for 3 and more MUBs, http://arxiv.org/abs/0909.3720.
- ^ a b c S. Wehner and A. Winter, 2010 New J. Phys. 12 025009: http://iopscience.iop.org/1367-2630/12/2/025009/.
- ^ S. Wu, S. Yu, K. Mølmer, Entropic uncertainty relation for mutually unbiased bases, Phys. Rev. A 79, 022104 (2009), http://arxiv.org/abs/0811.2298.
- ^ Ballester, M.; S. Wehner (2007). "Entropic uncertainty relations and locking: tight bounds for mutually unbiased bases". Physical Review A 75: 022319. http://arxiv.org/abs/quant-ph/0606244.
- ^ Wehner, S.; A. Winter (2008). "Higher entropic uncertainty relations for anti-commuting observables". Journal of Mathematical Physics 49: 062105. http://arxiv.org/abs/0710.1185.
- ^ a b S. Weigert, M. Wilkinson, Mutually Unbiased Bases for Continuous Variables, Phys. Rev. A 78, 020303(R) (2008), http://arxiv.org/abs/0802.0394.
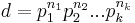
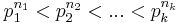
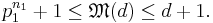
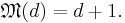
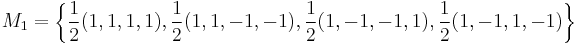
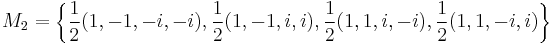
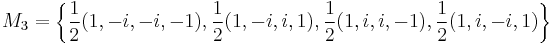
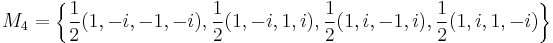
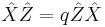
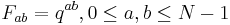
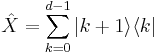
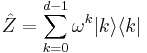
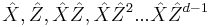
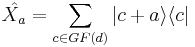
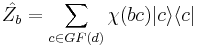
![\chi(\theta) = \exp \left [ \frac{2\pi i }{p} \left ( \theta%2B \theta^p %2B \theta^{p^2}%2B \cdots %2B \theta^{p^{M-1}} \right ) \right ],](/2012-wikipedia_en_all_nopic_01_2012/I/083713a8888dbf1d09f2f9a471455dfa.png)